なぜ偏微分を学ぶ？フーリエの熱伝導方程式を例に

どうも、木村（@kimu3_slime）です。

今回は、高校数学の微積分では扱わないけれども、大学数学で扱うテーマ、そのひとつが（多変数関数の）偏微分です。

今回は、熱が伝わる現象を説明する熱伝導方程式を例に、偏微分がなぜ必要かを紹介します。

単なる微分については：「運動」をイメージすればわかる、微分と積分入門、サイン、コサインは何の役に立つ？バネの振動と三角関数

運動方程式と熱方程式を見比べる

いきなりですが、すでに知られている2つの有名な方程式を眺めてみましょう。

\[ \begin{aligned}m\frac{d^2 x(t)}{dt^2}=F\end{aligned} \]

\[ \begin{aligned}\frac{\partial u(x,t) }{\partial t}= \Delta u\end{aligned} \]

\(d\)は（常）微分、\(\partial\)は偏微分の記号です。

上側はニュートンの運動方程式です。未知関数、位置（運動）を表す関数\(x\)は、時間のみを変数としています。未知関数の変数がひとつの微分方程式は、常微分方程式と呼ばれます。

下側は熱方程式です。細い針金や鉄板、空間を熱が伝わっていくようすを想像してみてください。未知関数、温度を表す関数\(u\)は、時間だけでなく位置の関数でもあります。未知関数の変数が2つ以上ある方程式は、偏微分方程式と呼ばれます。

運動方程式では、運動する物体が点とみなされています。点がどう動いていくかという話は、偏微分を使わずに、時間微分のみを扱った常微分方程式で書けるのです。

熱方程式では、熱の分布がどう変わっていくかを説明します。熱が熱いところから冷たいところへ伝わっていくという仕組みです。

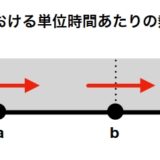
下の図を見てください。細い針金の中心を最初に温め、その熱が時間変化によって広がっていく（冷めていく）ようすを表しています。

（図の描写には、溝口純敏「Maximaを使った物理数学基礎ノート」を参考にしました。）

温度のグラフが凸となっているところが冷めて、凹となっているところが温まっていますね。熱方程式は、このような凸凹をなめらかにするルールと言うことができます。

熱の分布は、物体の運動のように点では表せません。「どんな形の熱分布をしているのか」が時間変化に影響しているのです（それが拡散項\(\Delta u\)の部分）。つまり、時間微分\(\frac{\partial}{\partial t}\)だけでなく、空間微分\(\frac{\partial}{\partial x}\)も式に組み込む必要があることがわかります。

拡散項は、次のような二回偏微分の足し合わせです。

\[ \begin{aligned}\Delta u = \sum _{k=1} ^{N} \frac{\partial ^2 u}{\partial x_k ^2} \end{aligned} \]

偏微分とは、微分する変数以外の変数を固定して行う微分のこと。例えば時間微分なら空間変数\(x\)を定数とみなしますし、空間微分なら時間変数\(t\)を定数をみなします。

グラフと\(\Delta u\)の式を見比べてみてください。ここでは空間は1次元なので\(N=1\)です。\(\Delta u=\frac{\partial ^2 u}{\partial x ^2}\)、二回微分は、グラフが凹となるところで正の値、グラフが凸となるところで負の値をとりますよね。これを時間そのときどきで計算していると考えれば、熱分布の変化も理解しやすいでしょう。

空間の次元を\(N=2,3\)とあげてみても、同様の熱分布が想像できるでしょうか？

熱方程式を導き出したのは、ジョゼフ・フーリエ（1768-1830）と言われています。

\[ \begin{aligned}\frac{\partial u(x,t) }{\partial t}= \Delta u\end{aligned} \]

フーリエはこの方程式を解くために、フーリエ級数やフーリエ変換という手法を生み出しました。それらは総じてフーリエ解析と呼ばれ、理工学全般でよく使われるツールとなっています。

また、細かい物質の拡散も、熱伝導方程式と全く同じ式に従うと言われています（拡散方程式）。これはフィックによるものですね。

なぜ偏微分を学ぶのか、少しはそのモチベーションをつかむことができたでしょうか。

運動方程式は比較的シンプルなルールで、その仕組みは外から受ける力のみによって決まっています。位置関数の時間変化は、位置関数の空間的な情報は参照しません（質点と仮定して考えている）。

一方で熱方程式、拡散方程式は、外側の情報のみによって変化するわけではありません。そのときそのときの熱分布・濃度分布、つまり解の空間分布に応じて時間変化していきます。時間変化と同時に、空間方向の形状もとらえるために必要なのが偏微分です。

熱分布や濃度分布を想像すれば、多変数関数の偏微分という分野も学びやすいのではないかと思います。

木村すらいむ（@kimu3_slime）でした。ではでは。